ABSTRACT
Ground motions characteristics of the 1887 Pinal de Amoles (MW = 5.53) and the 1989 Landa de Matamoros (MW = 4.94) Querétaro earthquakes were studied. For this purpose, the specific barrier model (SBM) was implemented in the context of the stochastic ground motion representation of earthquakes. The SBM was calibrated by modeling the peak ground acceleration (PGA) and the Fourier acceleration spectra (FAS) of the 11 May 2016 (MW = 4.80) Guadalajara earthquake. The calibration results showed that the SBM and selected source and path parameters were able to reproduce synthetic PGA and spectra in good agreement with observed waveforms; in particular, a stress drop of 160 bars fits the results better. Several rupture scenarios for the 1887 and 1989 events were performed by obtaining synthetic seismograms considering different values of stress drop (10, 30, 50, 100, 150, 200, 300, and 500 bars). For a typical stress-drop value of 100 bars, the PGA at distances of 10 and 200 km are in the following intervals: 2.57–295 cm/s2 and 1.72–186 cm/s2 for the Pinal de Amoles and Landa de Matamoros earthquakes, respectively. The results obtained in this study contribute toward a better understanding of strong ground motions in the region.
Keywords: Ground motion simulation; peak ground acceleration; specific barrier model; Mexico.
RESUMEN
Se estudiaron las características de los movimientos de terreno de los sismos de Pinal de Amoles de 1887 (MW = 5.53) y Landa de Matamoros de 1989 (MW = 4.94) en Querétaro. Para este propósito, se implementó el modelo de barrera específica (SBM) en el contexto de la representación estocástica del movimiento del suelo de los terremotos. El SBM se calibró modelando la aceleración máxima del suelo (PGA) y los espectros de aceleración de Fourier (FAS) del terremoto de Guadalajara del 11 de mayo de 2016 (MW = 4.80). Los resultados de la calibración mostraron que el SBM y los parámetros fuente y trayectoria seleccionados fueron capaces de reproducir los espectros y PGA sintéticos en concordancia con las formas de onda observadas; en particular, una caída de esfuerzos de 160 bares, ajusta mejor los resultados. Se realizaron varios escenarios de ruptura para los eventos de 1887 y 1989 mediante la obtención de sismogramas sintéticos considerando diferentes valores de caída de esfuerzos (10, 30, 50, 100, 150, 200, 300 y 500 bares). Para un valor típico de caída de esfuerzos de 100 bars, los PGA a distancias de 10 y 200 km están en los siguientes intervalos: 2.57–295 cm/s2 y 1.72–186 cm/s2 para los sismos de Pinal de Amoles y Landa de Matamoros, respectivamente. Los resultados obtenidos en este estudio contribuyen a una mejor comprensión de los movimientos fuertes del terreno en la región.
Palabras clave: simulación de movimientos fuertes; aceleración máxima del suelo; modelo de barrera específico; México.
Manuscript received: May 13, 2023
Corrected manuscript received: July 19, 2023
Manuscript accepted: July 22, 2023
INTRODUCTION
The State of Querétaro is located in the central segment of the Trans-Mexican Volcanic Belt (TMVB). The TMVB is a Neogene volcanic arc with a length of about 1000 km between 18.5°N and 21°W (Ferrari et al., 2012). The seismicity of the TMVB is not directly associated with the subduction zone but is due to multiple East-West striking normal faults (Suter, 1991; Suter et al., 1992, 1995a and 1995b). In particular, the State of Querétaro is classified as a region with a low seismicity rate. However, some intermediate earthquakes (M ~ 5.0) have taken place, such as the 1887 Pinal de Amoles earthquake (mb = 5.3) and the 1989 Landa de Matamoros earthquake, mb = 4.6 (Suter et al., 1996). The earthquakes in the State of Querétaro mainly originate in the crust at a shallow depth, which is why they can cause significant damage to the population and the infrastructure located in the epicentral zones. The seismicity reported in the state of Querétaro is characterized by earthquakes with magnitudes in the range of 0.7–5.3 (Suter et al., 1996; Zúñiga et al., 2003; Clemente-Chavez et al., 2013; León-Loya, 2014; Rodríguez-Pérez, 2022).
Calculating ground motions at a given site from a postulated earthquake of known magnitude is a fundamental problem for seismologists and earthquake engineers. Empirical relationships and physical models can be used to evaluate ground motion features. In the first approach, several ground-motion observations, such as peak values of displacement, velocity, and accelerations from different earthquakes with different characteristics, are used to construct a predictive equation (model). Although the empirical approach gives accurate predictions for regions with abundant data, it does not give us insights into the physical aspects of the earthquake rupture. In the second approach, ground motions are obtained by modeling earthquakes to describe the physics of seismic faulting based on limited observations. Here, the limited observations are used only to calibrate the physical model. Ground motion models are mainly developed in the context of the stochastic modeling approach (Boore, 2003) and random vibration theory. The seismic source, wave propagation parameters, and site effects must be known to evaluate reliable seismic hazards for a region using the physical method. Generally, Brune’s model is used to describe the seismic source, and Brune’s model represents the seismic radiation from a point source (Brune, 1970). However, a more precise source model is the specific barrier model (SBM) proposed by Papageorgiou and Aki (1983a, 1983b). Unlike Brune’s model, the SBM can be used to model heterogeneous rupture (Papageorgiou, 1988). Another advantage of the SBM is that the model can be used for both ‘near-source’ and ‘far-field’ strong ground motion simulations (Mavroeidis and Papageorgiou 2003; Mavroeidis et al., 2004). The SBM method is versatile because few parameters are required in the implementation. Incorporating this source model with suitable path and site effect models makes it possible to have a complete description of the ground-motion observations. In this article, the SBM is used to simulate the ground motions of the 1887 Pinal de Amoles and the 1989 Landa de Matamoros earthquakes. The results can help evaluate the seismic risk in the State of Querétaro.
TECTONIC SETTING
Here, some geological characteristics of the epicentral zones of the 1887 Pinal de Amoles and 1989 Landa de Matamoros earthquakes in the state of Querétaro are briefly described (Figure 1). Pinal de Amoles is located at the boundary of two geological provinces, the north-south striking late Cenozoic normal faults of northern Mexico and the region of east-west striking late Miocene to Quaternary normal faults typical for the TMVB. The former geological province is part of the Basin and Range province (Suter, 1987; Henry and Aranda-Gómez, 1992). In the epicentral region of the 1887 event, a north-south trending lineament 45 km long is observed, which is probably the expression of a late Cenozoic normal fault (Suter et al., 1996). According to Suter et al. (1996), the presence of this lineament and the north-south elongation of the inner-most calculated intensity contours support the hypothesis that the 1887 event took place on a north-south striking Basin and Range normal fault. On the other hand, the epicentral zone of the Landa de Matamoros earthquake is located within the Sierra Madre Oriental fold-thrust belt where the outcropping rocks are mostly limestones and shales in folds striking north-northwest-south-southeast (Carrillo-Martínez, 1989, 1990). The distance between the two epicenters is about 30 km, but it is unclear if the two events are related to the same fault system (Suter et al., 1996).

Figure 1. Earthquake locations of studied events. a) Epicenter location of the 1887 Pinal de Amoles and 1989 Landa de Matamoros earthquakes in Querétaro (color stars); b) Location of the 2016 Guadalajara earthquake (red star) and strong ground motion stations: GDLP, GDLC and CDGU (black triangles).
DATA AND METHODS
In this article, the SBM in the context of the stochastic method to simulate ground motions is implemented. First, the method was calibrated using an instrumentally recorded earthquake with similar characteristics to the target earthquakes, the 1887 and 1989 events. For the case of the 1989 earthquake, no seismic records were obtained, so the 11 May 2016 (MW = 4.8) Guadalajara earthquake was used to test and calibrate the SBM. This earthquake was selected because it is comparable in magnitude with the Landa de Matamoros event, tectonic environment (all events took place in the TMVB), and hypocentral depth. Once the SBM was implemented and calibrated, synthetic acceleration records and peak ground acceleration (PGA) curves were generated.
Data
Acceleration records of the Accelerographic Network of the Instituto de Ingeniería of the Universidad Nacional Autónoma de México (RAII-UNAM) were used. For the case of the 11 May 2016 (MW = 4.8) Guadalajara earthquake, three records were obtained, one at the rock site (station CDGU) and two at the soil sites (stations GDLC and GDLP). The station at the rock site is equipped with an ETNA Episensor accelerometer, sampled at 200 Hz (Kinemetrics, USA). On the other hand, the stations located at soil sites are instrumented with K2 accelerometers with a sampling frequency of 100 Hz (Kinemetrics, USA). The hypocentral distances of the three seismic stations are 21.77, 24.78, and 124 km (stations GDLP, GDLC, and CDGU, respectively). Figure 1 shows seismic stations and epicentral locations of all the earthquakes studied.
The Specific Barrier Model
The well-established stochastic modeling approach and random vibration theory to predict ground motions (Boore, 2003) were applied to determine ground motion features of analyzed earthquakes. In the frequency domain, the Fourier amplitude spectrum of displacement, Y(M0, r, f), for horizontal ground motions due to S-waves may be calculated as a product of the source spectrum E(M0, f), propagation path effects P(r, f), site effects G(f), and the type of motion considered, I(f) as:
Y(M0, r, f ) = E(M0, f )P(r, f )G(f )I(f ) (1)
where M0 is the seismic moment, f is the frequency, and r is the hypocentral distance. The instrumental control term I(f ) can be expressed as follows: I(f ) = (2πf )n, and n is equal to 0, 1, or 2 when related to displacement, velocity, and acceleration, respectively. The SBM was introduced by Papageorgiou and Aki (1983a, 1983b) for the quantitative description of heterogeneous seismic rupture (Papageorgiou, 1988). In the SBM, the earthquake rupture can be represented as an aggregate of circular subevents of equal diameter, 2ρ0 (or barrier interval), filling up a rectangular fault plane of length (L) and width (W), as shown schematically in Figure 2. As seismic rupture propagates, a stress drop (ΔσL) (or local stress drop) takes place in each subevent, starting from its center and spreading radially with a constant rupture velocity (VR). The source term can be expressed as:
E(M0, f ) = cS(M0, f )D(f, fmax) (2)
where D(f, fmax) is a low-pass filter with a cutoff frequency (fmax), c is a frequency-independent factor equal to FRθφV/(4πρβ3), where F is the free surface amplification (a factor equal to 2), Rθφ is the averaged radiation pattern (0.55 for S-waves), V is the partition onto two horizontal components (1/√2), ρ is the rock density, and β is the S-waves velocity. The source spectrum S(M0, f ) represents the average S-wave radiation of seismic waves from the source, which in this article is modeled by the specific barrier model.
The acceleration source spectrum using the specific barrier model may thus be expressed as (Papageorgiou, 1988; Halldorsson and Papageorgiou, 2005):

(3)
where N is the total number of subevents, T is the faulting duration for the whole rupture, and M⩪0i(f) is the far-field displacement spectrum of the individual subevent or subevent spectrum (Papageorgiou, 1988). The number of subevents fulfills the condition that the aggregate subevent moment is equal to the total seismic moment. The spatial distribution of cracks on the main fault is confined by the geometry of the fault plane, as indicated in Figure 2. The size of the subfault may be obtained from the following empirical relationship (Halldorsson and Papageorgiou, 2005): log 2ρ0 = -2.58 + 0.5MW.
The parameter ζ accounts for the observed deviation from self-similar scaling (with magnitude) of the high-frequency source spectral levels of earthquakes in interplate and extensional tectonic regimes as ζ = 102η with η = -0.12(MW – 6.3) (Halldorsson and Papageorgiou, 2005). The shear wave source displacement spectrum of a single subevent is approximated by the ω-square spectrum, written as:

(4)
where M0i = (16/7)ΔσLρ03 and f2 is related to the crack radius (ρ0) by the following expression: f2 = Csβ/2πρ0, where the parameter Cs depends on the ratio VR/β (1.72 ≤ Cs ≤ 1.85 for 0.7 ≤ VR/β ≤ 0.9) (Sato and Hirasawa, 1973; Aki and Richards, 1980).
The function D(f, fmax) in equation 2 accounts for the decay of acceleration spectral levels above fmax (Hanks, 1979; Papageorgiou and Aki, 1983a, 1983b; Papageorgiou, 1988). The fmax filter is defined as
D(f, fmax) = [1+(f/fmax)2s]-1/2, where s controls the decay rate above fmax and is usually taken as s = 4 (Boore, 1983). Alternatively, Anderson and Hough (1984) showed that the onset of high-frequency spectral decay could be characterized by an observational parameter κ (or κ filter). The κ filter is defined as: D(f, κ) = A(f ) exp(-πκf ), A( f ) accounts for site amplification derived from several techniques such as the H/V ratio or theoretical generic rock site amplification functions (Boore and Joyner, 1997). Here, both filters in an application were combined, as Boore (2003) suggested. The path attenuation function P(r, f ) includes both regional anelastic and scattering attenuation (DQ(r, f ) = exp(-πrf/Q( f )β) where the quality factor is Q( f ) = Q0f n), and geometric spreading effects expressed as: D(r) = r-k. The next step of the ground motion simulation is constructing a random-phase signal in the time domain and multiplying it by a seismic wave-like shaping window. The shaping window applied to the noise can be either a simple box window or a window that gives a more realistic shape for the acceleration time series, such as the Saragoni-Hart function (Saragoni and Hart, 1974).

Figure 2. Schematic representation of the SBM. The fault plane is made up of the aggregate of circular cracks with a diameter 2ρ0 on a fault plane (A = LW).
A local stress drop (ΔσL) occurs in each crack as it ruptures. The rupture begins at the center of each crack. It spreads radially outward (the light circles denote the rupture fronts at successive time instants) until the barriers stop it, denoted by the shaded area between the cracks (modified from Halldorsson and Papageorgiou, 2005).
Ground motion calibration
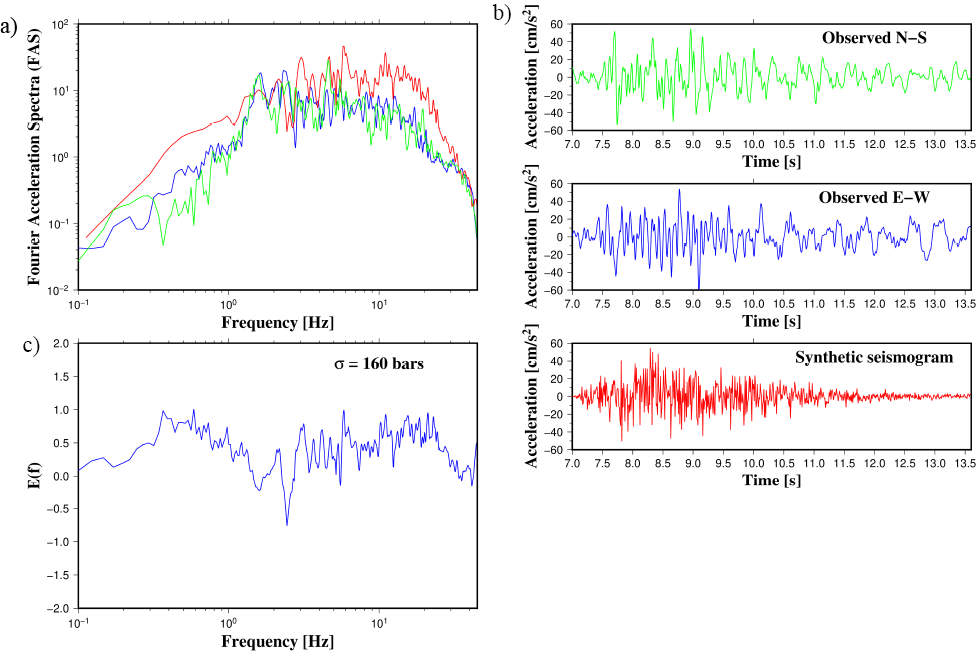
The SBM method was tested and calibrated by simulating ground motions from the 11 May 2016 (MW = 4.8) Guadalajara earthquake. Singh et al. (2017) studied source and ground motion characteristics from this event. To model this event, the results of Singh et al. (2017) were considered as input parameters for the SBM: ρ = 2850 kg/m3,
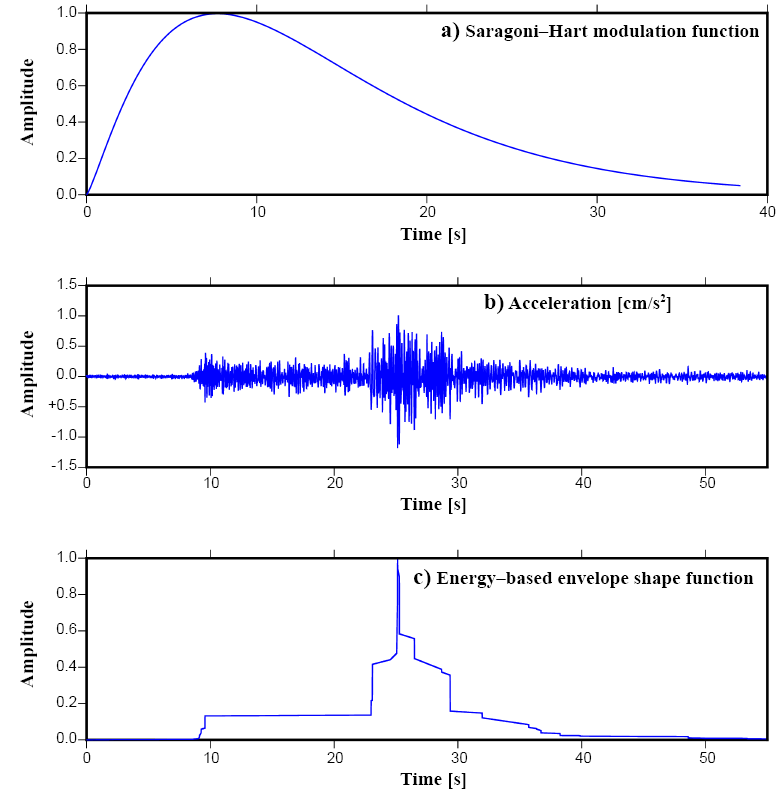
β = 3.8 km/s, L = 3.5 km, W = 3.5 km, VR = 3.7 km/s, κ = 0.01 s, and Q( f ) = 141f0.63. D(r)= 1/r for r ≤ 70 km and 1/(70r)0.5 for r > 70 km. Site amplifications were taken from generic rock and soil functions estimated by Boore and Joyner (1997), shown in Table 1. The amplifications are based on shear velocity and density as functions of depth obtained from borehole data and crustal velocity studies. The amplifications are computed using the quarter-wavelength approximation (Joyner et al., 1981). For a particular frequency, the amplification is given by the square root of the ratio between the seismic impedance averaged over a depth and the seismic impedance at the depth of the source. A simplified representation of the path duration TP in seconds was adopted as TP = 0.16(r – 10) for r < 70 km and Tp = 9.6 – 0.03(r – 70) for 70 ≤ r < 130 km, where r is the hypocentral distance in km (Atkinson and Boore, 1995). The simulations used two envelope functions: 1) Saragoni-Hart type function and 2) empirical envelope shape functions that are directly defined based on the energy distribution profile of given earthquake records based on Li et al. (2017), as shown in Figure 3.
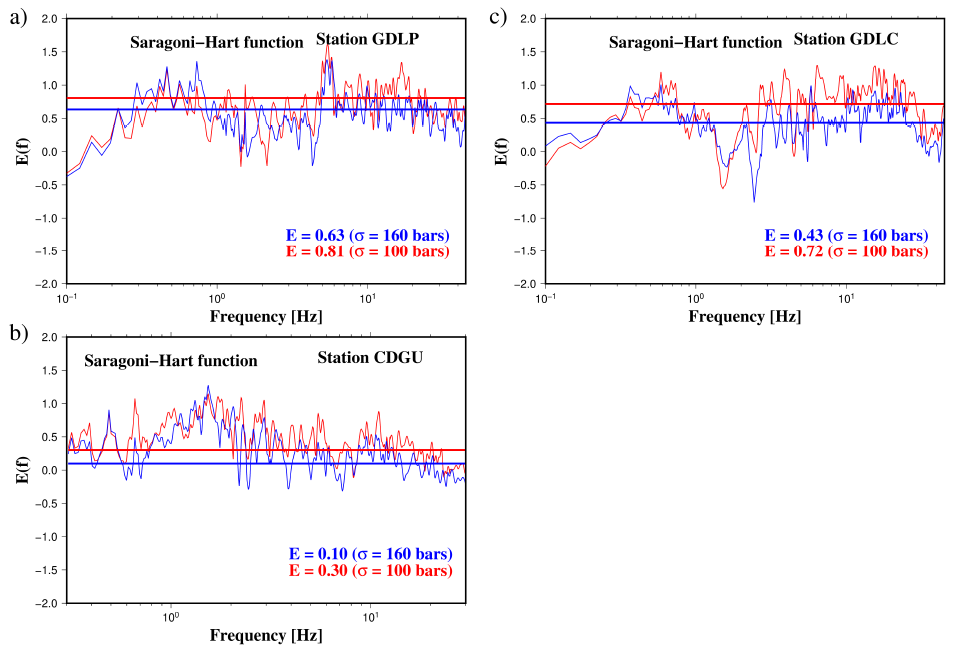
To generate synthetic accelerograms, ΔσL was varied (from 30 to 300 bars), looking for the best stress drop value to fit better the synthetic and observed records (Figures 4 to 9). The best fit was obtained with a stress drop of 160 bars, and this value is similar to the value of 100 bars reported by Singh et al. (2017). A spectral error function introduced by Castro et al. (2008) was also used to calculate differences between observed and synthetic acceleration spectra (Figures 4 to 9). The error function is defined as:
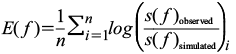
, (5)
where n is the number of stations/components modeled, and S( f ) is the acceleration spectra. Figures 10 and 11 show the comparison of error functions for results considering stress-drop values of 160 and 100 bars using the Saragoni-Hart and energy-based envelope functions. The spectral match is consistent with the observations of the 2016 Guadalajara earthquake. In terms of the peak accelerations, both envelope functions can simulate comparable PGA values, as shown in Figure 12. The logarithmic ratio between observed and calculated maximum accelerations is lower than 0.3. The Saragoni-Hart envelope function is able to characterize ground motions of the most energetic part of the seismogram after the S-waves (Figures 7 to 9). On the other hand, the energy-based envelope function generates more realistic synthetic seismograms, including motions before the S-waves (Figures 4 to 6). The simulation results indicate that the SBM can be used to model historical earthquakes lacking instrumental records.